top of page

Linear System of Equations
Linear System of Equations
System of equations of form
a1x + b1y + c1z = d1
a2x + b2y + c2z = d2
a3x + b3y + c3z = d3
is called a linear system of equation.
In the matrix form above system of equation is written as:
Linear System of Equations

Vector X is such that on linear transformation with matrix M, it lands on vector D.

Here X is unknown while D and M are known. So if we perform inverse transformation of M on D, we can find X.
Learn Basics:
Consistency of Linear System of Equations
Case 1:
For |M| ≠ 0, there always exists a unique vector X which after linear transformation lands on vector D. In this case, there exists a single unique solution of system of equations.
Case 2:
For |M| = 0, unit vector i and j become collinear after transformation and 2-D plane is reduced to a line.
-
If vector D lies on the same line as iT and jT, then system of equation has infinitely many solution.
Consistency of system

-
If vector D does not lie on the same line as iT and jT, then system of equation is inconsistent amd no solution exists.

For a zero determinant matrix, whether solution exists or not is determined by the concept of rank.
Rank of a Matrix
For a linear transformation matrix, rank is defined as number of dimensions in the output of transformation.
Consider a 2x2 square matrix. It may transform a 2-D plane such that:
-
iT and jT (unit vector i and j after transformation) remain in one plane but are not collinear. Number of dimension in the output of transformation is 2, hence rank is 2.
Rank


-
iT and jT become collinear after transformation. No of dimension in the output is reduced to 1, hence rank is 1.


-
iT and jT are reduced to a point after linear transformation. Since origin remain fixed in linear transformation, hence iT and jT both shift to origin. For this case rank of the matrix is zero.
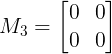

Similarly for a 3x3 matrix rank may be 3 (output dimension after transformation is 3), 2 (3-D space is reduced to a 2-D plane), 1 (3-D space is reduced to a line after transformation) or 0 (space is reduced to a point after transformation).
To find rank, matrix is converted into echelon form. No of non-zero rows (rows having minimum one element as non-zero) in echelon form is called rank of the matrix.
* For a non-singular square matrix (|M| ≠ 0), rank is always equal to number of columns of the matrix.
Consistency of Linear System of Equation
Consider a linear system of equation MX = D. For this system augmented matrix MA is defined as

A) System of equation is consistent if r(MA) = r(M)
i) If r(MA) = r(M) = number of unknows, system of equation has unique solution.
ii) If r(MA) = r(M) < number of unknows, system of equation has infinite number of solution.
B) System of equation is inconsistent if r(MA) ≠ r(M): No solution exists.
Example 1:
GATE 2018: The rank of matrix M (as given below) is
A) 1
B) 2
C) 3
D) 4
Previous years questions
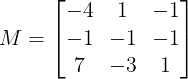
Solution:
|M| = -4(-1-3) -1(-1+7) -1(3+7) = 0
Since determinant of matrix is zero, hence this is not a full rank matrix. Linear transformation will reduce the space either to a plane or to a line.
r(M)<3
Unit vector i, j and k lands to iT, jT and kT after linear transformation:
iT = column vector C1 of matrix = -4i -j +7k
jT = column vector C2 of matrix = i - j -3k
kT = column vector C3 of matrix = -i -j +k
From the above, it is clear that all vectors lie in a plane y = -1. Hence after transformation ouput dimensions are 2 only.
So, rank of matrix r(M) = 2
Option B is the correct answer.
Example 2:
GATE 2005: A is a 3x4 real matrix and Ax = b is an inconsistent system of equation. The highest possible rank of A is:
A) 1
B) 2
C) 3
D) 4
Solution: Consider a 3x4 real matrix A as:
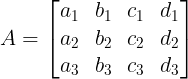
For system of equation Ax = b, augmented matrix of A:b will be a 3 x 5 matrix. In echelon form maximum number of non-zero rows for augmented matrix may be 3. Hence, maximum rank of augmented matrix is 3.
Now since the system of equation is inconsistent:
r(A) ≠ r(A:b)
So maximum rank of A may be 2.
Option B is the correct answer.
Example 3:
GATE 2001: The rank of a 3x3 matrix C=(AB), formed by multiplying a nonzero column matrix A of size 3x1 and a nonzero row matrix B of size 1x3 is
A) 0
B) 1
C) 2
D) 3
Solution: Consider matrix A and B as
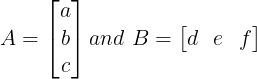

For matrix C, transformed i, j and k vectors are given as:
iT = d*(ai + bj + ck)
jT = e*(ai + bj + ck)
kT = f*(ai + bj + ck)
It is observed from the above, that all three unit vectors become collinear after transformation. Hence, output dimension after transformation is 1.
So r(C) = 1
Option B is the correct answer.
Example 4:
GATE 1999: Rank of the matrix M (given below) is:
A) 1
B) 2
C) 3
D) √2

Solution: For matrix M column vector is given as:
iT = 3i - 6j + 12k = 3(i - 2j + 4k)
jT = 2i - 4j + 8k = 2(i - 2j + 4k)
kT = -9i + 18j -36k = -9(i - 2j + 4k)
It is observed from the above that all three unit vectors become collinear after transformation. Hence, output dimension after transformation is 1.
So r(M) = 1
Option A is the correct answer.
Example 5:
GATE 2019: The set of equations
x + y + z = 1
ax - ay + 3z = 5
5x - 3y +az = 6
has infinite solution if a =
A) -3
B) 3
C) 4
D) -4
Solution: System of equation may be written in matrix form as AX = D
where;
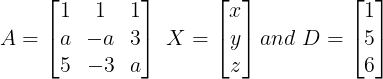
Since system of equation has infinite solution, determinant of A must be zero.
|A| = 1(-a*a + 9) -1(a*a - 15) + 1(-3a + 5a) = 0
- a^2 + 9 - a^2 + 15 + 2a = 0
2a^2 - 2a - 24 = 0
a^2 - a - 12 = 0
(a-4)(a+3) = 0
a = 4, -3
For a = 4, augmented matrix A:D is
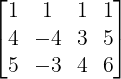
Convert to echelon form


r(A) = r(A:D) = 2
Hence system of equation has infinitely many solution for a = 4.
Similarly for a = -3, augmented matrix A:D in echelon form is

r(A) = 2 but r(A:D) = 3
Hence system of equation is inconsistent for a = -3.
Option C is the correct answer.
Example 6:
GATE 2016: The solution to the system of equations as given below is
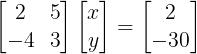
A) 6,2
B) -6,2
C) -6,-2
D) 6,-2
Solution: For system of equation Ax = B, x is found out by
Matrix of cofactors of A
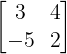
Adjoint of A

Inverse of A

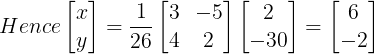
Hence correct answer is option D.
Example 7:
GATE 2012: The system of algebraic equations given below has
x + 2y + z = 4
2x + y + 2z = 5
x - y + z = 1
A) a unique solution of x = 1, y = 1, z = 1
B) only two solutions of (x = 1, y = 1 & z = 1) and (x = 2, y = 1, z = 0)
C) infinite number of solution
D) no feasible solution
Solution: System of equation may be written in matrix form as Ax = B
where;
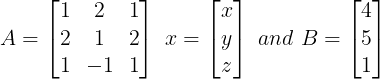
|A| = 1(1+2) -2(2-2) +1(-2-1) = 0
Since determinant of A is zero, hence system of equation will have either infinite solution or no solution.
Augmented matrix A:B is

Echelon form of A:B is
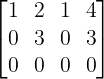
r(A) = r(A:B)
Hence system of equation has infinite solution.
Option C is the correct answer.
Example 8:
GATE 2011: Consider the following system of equations
2x1 + x2 + x3 = 0
x2 - x3 = 0
x1 + x2 = 0
This system has
A) A unique solution
B) No solution
C) Infinite number of solutions
D) Five solutions
Solution: System of equation in matrix form is written as

|A| = 2(0+1) - 1(0+1) + 1(0-1) = 0
Since this is a homogeneous system of equation and |A| = 0, hence it has infinite no of solutions.
Option C is the correct answer.
*Note: Homogeneous system of equations either have unique solution (|A| ≠ 0) are infinite number of solution (|A| = 0).
Example 9:
GATE 2008: For what value of a, if any, will the following system of equations in x, y and z have a solution
2x + 3y = 4
x + y + z = 4
x + 2y − z = a
(A) Any real number
(B) 0
(C) 1
(D) There is no such value
Solution: System of equation in matrix form Ax = B is written as:

|A| = 0
Augmented matrix A:B is written as

Augmented matrix in echelon form is
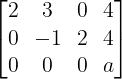
For solution to exist rank of A and A:B should be equal.
Since r(A) = 2, hence r(A:B) = 2 for which a = 0
Option B is the correct answer.
bottom of page

