top of page

Inverse of a Matrix
Determinants
Determinants of a matrix [M] is denoted as |M| and is calculated as:
-
For a 2 x 2 matrix
Determinants

Determinant = ad - bc
-
For a 3 x 3 matrix

Determinant = a(ei - fh) - b(di - fg) + c(dh - eg)
Physical Significance
Consider a square formed by unit vectors i and j in x-y plane. Area of this square is 1 unit sq. A 2 x 2 matrix M, transforms this space and shifts i and j to


Square formed by i and j is transformed into a parallelogram of area 5 unit sq. This change in area caused by linear transformation matrix is called determinant of the matrix.
For a 3 x 3 matrix, determinant represents change in volume of a unit cube formed by unit vectors i, j and k transformed by the matrix.
Learn Basics: Matrix as linear transformation of Vectors
Note the following special cases:
-
Zero Determinant: Either iT and jT become collinear or are reduced to a point (area becomes zero after transformation). For a 3 x 3 matrix, zero determinant means volume becomes zero after transformation which means that iT, jT and kT becomes co-planar or collinear or are reduced to a point.
-
Negative Determinant: i to j direction is anticlockwise for the above graph. If after transformation this direction is reversed then determinant will be negative.
Properties of Determinants
-
On exchanging rows of a determinant with corresponding columns, value of determinant remains same.
-
If any two rows (or two columns) of a determinant are exchanged, sign of changes but value remains same.
-
|M1M2| = |M1||M2|
-
If all elements of a determinant are multiplied by a value c, then the value of determinant is multiplied by c.
Cofactor of a Matrix
For a 3 x 3 matrix [aij] where i = 1,2,3 and j = 1,2,3; cofactor of element aij is:
Cofactor

Adjoint of a Square Matrix
Transpose of matrix [C] formed by cofactors of corresponding elements of a matrix [M].
Inverse of a Square Matrix
If A and B are two square matrix of same order such that [A][B] = I, then B is called inverse of matrix A.
Adjoint
Inverse
Inverse of a matrix is defined only if |A| ≠ 0.
Physical Significance
If a vector u is transformed to vector v by matrix M, inverse of M is a linear transformation matrix which brings vector v back to u.

Inverse of M is defined such that:
It is clear from the above figure that if determinant of M is zero, iT and jT will become collinear and for this case we can not define an inverse which will transform the space back to its original position.
Example 1:
GATE 2015: If any two columns of a determinant P are interchanged, which one of the following statments regrading the value of the determinant is correct.
A) Absolute value remains unchanged but sign will change
B) Both absolute value and sign will change
C) Absolute value will change but sign will not change
D) Both absolute value and sign remain unchanged
GATE previous questions

Solution:
Option A is the correct answer.
Example 2:
GATE 2014: Given that the determinant of matrix A is -12, the determinant of matrix B is, if A and B are as given below:

A) -96
B) -24
C) 24
D) 96
Solution:
If each element of a row (or column) of a matrix is multiplied by k, the value of determinant is multiplied by k. Here, matrix B is obtained by multiplying 2 in each row of the matrix, hence value of determinant is multiplied by 2x2x2 = 8.
|B| = 8*|A| = 8*(-12) = -96
Option A is the correct answer.
Example 3:
GATE 2018: For the following matrix A, find determinant of inverse of A.

Solution:
|A| = 1(4-0) + 0 + 0 = 4
Hence matrix A transforms a unit volume in space such that final volume is 4 unit. Inverse of A will reverse back this transformation and final volume will again become 1 unit. Hence;
Example 4:
GATE 2015: For a matrix P as given below, the inverse of P is





Solution:
Cofactors of elements
C11 = (-1)^(1+1) * (4-3i) = 4-3i
C12 = (-1)^(1+2) * (i) = -i
C21 = (-1)^(2+1) * (-i) = i
C22 = (-1)^(2+2) * (4+3i) = 4+3i
Matrix of Cofactors =
_edited.png)
Adjoint of matrix P = Transpose of matrix C =
_edited.png)
Inverse of matrix P = adj P/|P|
|P| = (4+3i)(4-3i) + i*i = 24
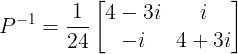
Hence option A is the correct answer.
bottom of page

