
Matrix: An Introduction
Matrix:
Collection of numbers arranged in rows and columns. An 'm x n' matrix has m rows and n columns.
A 2 x 3 matrix having 2 rows (arranged horizontally) and 3 columns (arranged vertically) is represented as:

Matrix as linear transformation of vectors:
A matrix may be represented as linear transformation of vectors in space. Consider a 2x2 matrix

This is a linear transformation matrix for a vector in 2-D plane. If 'i' and 'j' are unit vectors along x-axis and y-axis respectively, then column 1 of the above matrix represents position vector of transformed 'i' and column 2 represents position vector of transformed 'j'.

i (transformed) = 2*i + 0*j = 2i
j (transformed) = 1*i + 1*j = i+j
For example a vector V = 2i + 3j is transformed by Matrix M as follows:



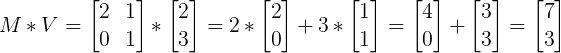
Example:
GATE 2019: The transformation matrix for mirroring a point in x-y plane about the line y = x is given by

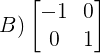
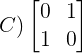

Solution:
Transform matrix is such that, all transformed vectors in x-y plane are mirror image of original vector. First task is to find out transformed unit vectors 'i' and 'j'.

Mirror image of 'i' about line y = x is 'j' and mirror image of 'j' about same is 'i'.
Hence,
i (transformed) = j = 0*i + 1*j
j (transformed) = i = 1*i + 0*j
In matrix form above transformation may be written as:

Hence the correct answer is 'C'.
Example:
GATE 2014: Which one of the following equation is correct identity for arbitrary 3x3 real matrix P, Q and R.
A) P(Q + R) = PQ + RP
B) (P - Q)^2 = P^2 - 2PQ + Q^2
C) Det (P + Q) = Det P + Det Q
D) (P + Q)^2 = P^2 + PQ + QP + Q^2
Solution:
P(Q + R) = PQ + PR
(P-Q)^2 = P^2 - PQ - QP + Q^2
Det (P + Q) ≠ Det P + Det Q
(P+Q)^2 = P^2 + PQ + QP + Q^2
Hence option D is the correct answer.

