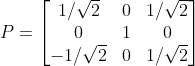Matrix: Types
Transpose of a Matrix:
Matrix formed by exchanging rows and corresponding columns of the original matrix. Transpose of a matrix A:
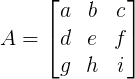

Hence; (a)ij of [A] = (a)ji of transpose of [A], where (a)ij is element in ith row and jth column and (a)ji is element in jth row and ith column.
* Value of determinant of [A] and transpose of [A] is same i.e. lAl = lTrans. Al
Null Matrix:
Matrix having all the elements as zero.

This matrix transforms all vectors in the space to zero vector i.e. at the origin.
Square Matrix:
Matrix having equal number of rows and columns. A 2 x 2 matrix is:

2 x 2 square matrix transforms a 2-D vector such that it remains in 2-D plane only. Likewise, a 3 x 3 square matrix transforms a 3-D vector such that remains in 3-D space only. Whereas a non-square matrix may transform a 2-D vector into 3-D vector and vice-versa.
Diagonal Matrix:
A square matrix having only non-zero diagonal elements. All other elements of the matrix are zero.

A diagonal matrix is called 'Scalar Matrix' when a = b. A scalar matrix only stretches or shrinks a vector along its span.
A diagonal matrix is called a 'Unit/Identity Matrix' if a = b = 1. Unit matrix is represented by I and does nothing to the vector after transformation. A 3x3 unit matrix is:
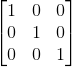
Symmetric and Skew-Symmetric Matrix:
A square matrix is called 'Symmetric' if
(a)ij = (a)ji
Hence; Trans.[A] = [A]
A 3 x 3 symmetric matrix is:

For a 'Skew-Symmetric Matrix'
(a)ij = -(a)ji and (a)ii = 0
Hence;Trans.[A] = -[A]
A 3 x 3 skew-symmetric matrix is:

Orthogonal Matrix:
A square matrix satisfying the condition
An orthogonal matrix transforms a space such that axes always remains perpendicular to each other and magnitude of unit vectors remains unchanged (rotation/reflection). Consider an orthogonal matrix:
For the above matrix
so i(transformed) and j(transformed) are perpendicular to each other and their magnitude is equal to 1.
* Value of determinant of an orthogonal matrix is equal to 1 or -1 i.e. lAl = 1 or -1.
Idempotent Matrix:
For an idempotent matrix
Nilpotent Matrix:
For a nilpotent matrix
k is a positive integer.
Least positive integer for which above value is true is called index of the matrix.
Involuntary Matrix:
For an involuntary matrix
It means matrix is inverse of itself.
Singular Matrix:
A matrix is called a singular matrix if its determinant is zero i.e. lAl = 0.
Triangular Matrix:
A square matrix having all elements below the main diagonal as zero is called 'Upper Triangular (UT) Matrix'. For upper triangular matrix (a)ij = 0 for all i>j.

A square matrix having all elements above the main diagonal as zero is called 'Lower Triangular (LT) Matrix'. For lower triangular matrix (a)ij = 0 for all i<j.

* Transpose of a LT Matrix is a UT matrix.
* Determinant of triangular matrix is equal to product of diagonal elements.
Complex Matrices:
Matrix whose elements may be complex numbers.
a) Conjugate of a Matrix:
Matrix formed by conjugates of complex elements of original matrix.
b) Conjugate Transpose:
Transpose of conjugate of a complex matrix.
c) Unitary Matrix:
A complex square matrix is said to be Unitary when product of the matrix (A) with its conjugate transpose (A*) is equal to an identity matrix i.e. AA* = I
d) Hermitian Matrix:
A complex square matrix is called hermitian if (a)ij = conjugate of (a)ji. A 2 x 2 Hermitian matrix is:
For a Hermitian matrix A = A*. Diagonal elements of the matrix will always be either real or zero.
e) Skew-Hermitian Matrix
A complex square matrix is called Skew-Hermitian if (a)ij = - conjugate of (a)ji. A 2 x 2 Skew-Hermitian matrix is:
For a Skew-Hermitian matrix A = -A*. Diagonal elements of the matrix will always be either zero or pure imaginary.
Example:
GATE 2016: A real square matrix A is called skew-symmetric if
Answer: C
Example:
GATE 2009: For a Matrix [M] as given below, the transpose of the matrix is equal to the inverse of the matrix. The value of x is:
A) -4/5
B) -3/5
C) 3/5
D) 4/5
Solution:
Since Trans. of [M] = Inv. of [M], so the matrix is an orthogonal matrix. Hence column vectors will be perpendicular to each other and their magnitude will be equal to 1.
Column 1 vector C1 = 3/5 i + x j
Column 2 vector C2 = 4/5 i + 3/5 j
For perpendicularity of C1 and C2: (3/5)*(4/5) + (x)*(3/5) = 0
Hence x = -4/5
The correct answer is Option 'A'.
Example:
GATE 2006: Multiplication of matrices E & F is G. Matrix E and G are as given below. What is the matrix F?



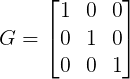
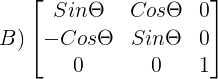

Solution:
For matrix E: Column vector C1, C2 and C3 are perpendicular to each other (vector dot product is zero) and magnitude of each column vector is 1. Hence matrix E is Orthogonal matrix.
For orthogonal Matrix E x (Trans. of E) = I
Here it is given as E x F = G, where G is identity matrix.
Hence F must be transpose of E.
The correct answer is option 'C'.
Example:
GATE 2004: For which value of x, the matrix given below will become singular:

a) 4
b) 6
c) 8
d) 12
Solution:
For a singular matrix lAl = 0
8*(0-12) - x*(0-24) + 0 = 0
-96 + 24*x = 0
x = 4
The correct answer is option 'A'.
Example:
GATE 2017: Consider the matrix P as given below. Which one of the following statements about P is incorrect.
A) Determinant of P is equal to 1.
B) P is orthogonal.
C) Inverse of P is equal to its transpose.
D) All eigenvalue of P are real numbers.